

) Unlike the previous method, the mthode du balayage of Poincar uses approximation functions each of. The fundamental theorem of calculus relates antidifferentiation with integration. ( See his paper in the Acta Mathematica, Vol. The reverse process is called antidifferentiation. The process of finding a derivative is called differentiation.

For a real-valued function of several variables, the Jacobian matrix reduces to the gradient vector. It can be calculated in terms of the partial derivatives with respect to the independent variables.
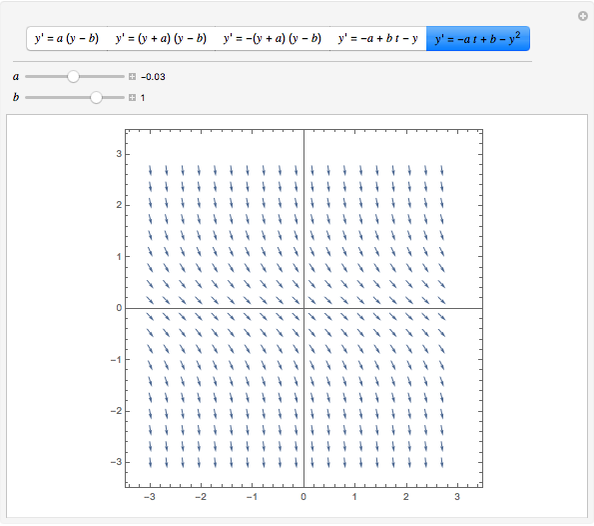
The Jacobian matrix is the matrix that represents this linear transformation with respect to the basis given by the choice of independent and dependent variables. In this generalization, the derivative is reinterpreted as a linear transformation whose graph is (after an appropriate translation) the best linear approximation to the graph of the original function. Each equation has a family of solutions parametrized by the parameter. This Demonstration shows Bernoulli's equation and solutions for a few choices of and. For this reason, the derivative is often described as the "instantaneous rate of change", the ratio of the instantaneous change in the dependent variable to that of the independent variable.ĭerivatives can be generalized to functions of several real variables. Substituting and, we get the linear differential equation. The tangent line is the best linear approximation of the function near that input value. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. For example, the derivative of the position of a moving object with respect to time is the object's velocity: this measures how quickly the position of the object changes when time advances. However, in our teaching we have found that it is helpful to have further documentation of the various solution techniques introduced in the text. Derivatives are a fundamental tool of calculus. New Differential and Integral Equations Functions. This solution will be the solution to the differential equation itself. Gives a uniformly coordinated collection of examples and problems where the use of Mathematica amplifies the content of the material.In mathematics, the derivative shows the sensitivity of change of a function's output with respect to the input. FEM method y(x) to a functional J(y(x)) y(x) minimizes this functional. Finance, Statistics & Business Analysisįor the newest resources, visit Wolfram Repositories and Archives »ĭifferential Equations: An Introduction with MathematicaĪbout Differential Equations and Linear Algebra | First-Order Differential Equations | Applications of First-Order Equations | Higher-Order Linear Differential Equations | Applications of Second-Order Equations | The Laplace Transform | Higher-Order Differential Equations with Variable Coefficients | Differential Systems with Constant Coefficients | Differential Systems with Variable Coefficients | AppendixĪn introductory sophomore/junior level text in differential equations suitable for students in mathematics, physics, and engineering.Wolfram Knowledgebase Curated computable knowledge powering Wolfram|Alpha.

Wolfram Universal Deployment System Instant deployment across cloud, desktop, mobile, and more. Wolfram Data Framework Semantic framework for real-world data.


 0 kommentar(er)
0 kommentar(er)
